2-2. Jensen's 와 Fano's inequality 및 충분 통계량

출처: Elements of Information Theory - Second Edition, Thomas M. Cover & Joy A. Thomas

 

2.1 Jensen's inequality와 이에 대한 결과

 

두 파트로 나누어진 2장에서 후반부에 해당하는 2-2는

옌센의 부등식 (Jensen's inequality)을 다루면서 시작할 것이다.

 

 

그 전에, convex function이란 개념에 대해 다룬다.

다음과 같이 $(a,b)$사이에서 아래로 볼록한 성질 (convex)을 갖는 함수 (function) $f(x)$에 대해서 다음 수식을 만족한다.

이때, $x_1$과 $x_2$는 $(a,b)$범위안에 있으며 $\lambda$의 값은 0과 1사이에 있다 $(0 \leq \lambda \leq 1)$.

 

 

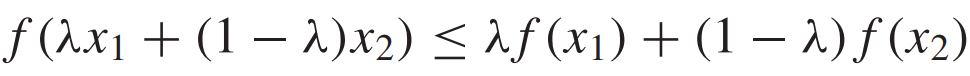
이때, function $f(x)$가 strictly convex라면, $\lambda=0$혹은 $\lambda=1$일때 등호 (equality)가 성립한다.

strictly convex의 의미는 위의 식에서 등호만 제외하고 부등호만 존재하는 수식인 경우를 말한다.

자세한 내용을 <convex optimization>에 다룬다.

또한, 만약 $-f$가 convex라면, function $f$는 위로 볼록(concave)이다.

 

 

 

---

 

 

 

대표적인 convex function으로 다음과 같은 function이 있다 $(0 \leq x)$.

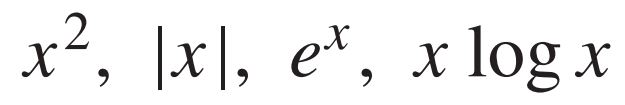
또한, 대표적인 concave function으로 다음과 같은 function이 있다 $(0 \leq x)$.

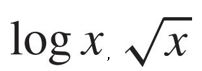
이러한 대표 function들의 그림을 그리면 아래와 같다.

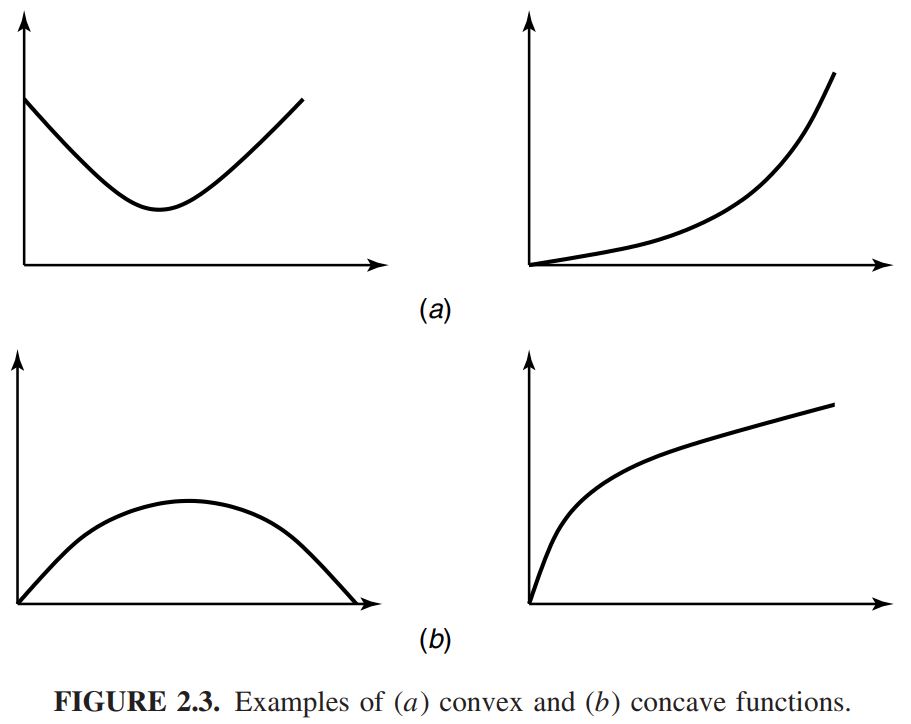
그럼, 다음과 같은 질문을 할 수 있다.

 

 

 

해당 function들은 가장 기본적인 function인데, 만약 더욱 복잡한 function $f$가 존재한다고 하자.
이때, $f$가 convex인지 혹은 concave인지 어떻게 알 수 있을까?



 

이는 다음과 같은 정리 (theorem)으로 정의할 수 있다.

만약 function $f$가 어떤 구간(interval) 내에서 "음이 아닌 이차 도함수(non-negative second derivative)"를 갖는다면,

그 function $f$는 해당 구간에서 "convex (혹은 strictly convex)"이다.

이에 대한 증명은 다음과 같다.

 

 

먼저, 어떤 function $f$가 미분가능하다고 하자.

또한, function $f$의 어떤 구간 내에 점 (point) $x_0$가 존재한다고 하자.

이때, 우리는 $x_0$라는 점을 이용하여

function $f$를 다음과 같이 "테일러 급수 전개 (Taylor series expansion)"를 사용한다.

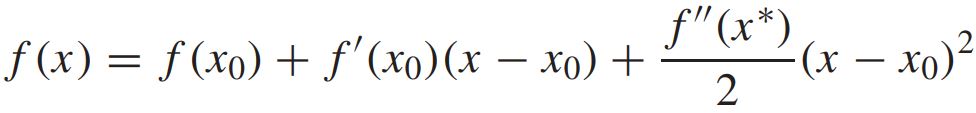
 여기서 $x^{*}$은 $x_0$와 $x$사이에 있는 점을 말한다.

 

만약, $0 \leq f''(x^{*})$이라면, 전체 수식에서의 마지막 항 (term)은 모든 $x$에 대해서 non-negative이다. 

여기서 아래와 같이 $x_0$를 정의해보자.

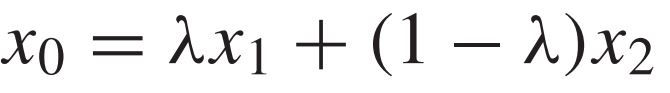
이때 $x=x_1$이라 한다면, 우리는 아래의 수식을 얻을 수 있다.

1번

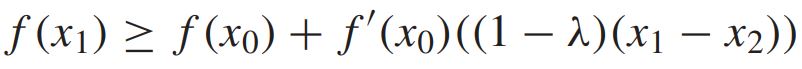
이와 유사하게 $x=x_2$라 한다면, 아래의 수식을 얻을 수 있다.

2번

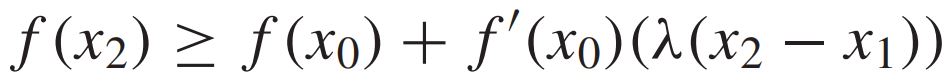
1번 수식에 $\lambda$를, 2번 수식에 $1 - \lambda$를 곱하여 두 수식을 더하면, 가장 맨위에 있는 수식을 만족한다. ∎

 

이렇게 정의한 convex function을 이용하여 Jensen's inequality에 대해 정의하자.

만약 function $f$가 convex function이고 확률변수 $X$가 있다고 하자.

이때, 다음 수식을 만족하는데, 이를 "Jensen's inequality"라고 한다.

 

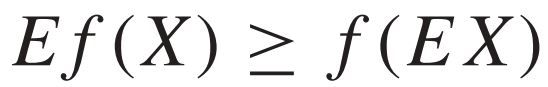
여기서 E 는 expectation을 의미한다.

 

---