Elements of Information Theory - Second Edition, Thomas M. Cover & Joy A. Thomas
1.1 정보이론이란?
"정보"라는 것에 대한 "수학적인 이론"을 말한다.
여기서 "정보"라는 것은 일반적으로 message (speech, text, images, etc.)를 수신함으로써 얻는다.
그럼 message로부터 정보를 얻을 때, 다음과 같은 물음이 있을 수 있다.
수신된 message의 의미는 무엇인가?
얼마나 이 message가 중요한 것인가?
이 message에서 내가 얻을 수 있는 정보량은 얼마나 되는가?
이중에서 정보이론에서는 오로지 "message에서 내가 얻을 수 있는 정보량은 얼마나 되는가?"란 질문에 답을 한다.
이러한 특징이 바로 정보이론의 핵심이며, 정보 전달 측면에서 시스템의 근본적, 이론적 한계를 분석한다.
1.2 통신에서의 정보이론
1940년대까지만 하더라도 오류 확률을 무시할 정도의 positive rate로 정보를 전송하는 것이 불가능하다고 생각했다.
그러나 Shannon은 채널 용량(channel capacity)보다 작은 모든 통신 속도에 대해 오류 확률을 거의 0으로 만들 수 있다는 사실을 증명했다.
또한, 음악 (music) 및 음성 (speech)과 같은 무작위 과정 (random process)은 신호가 압축 (compress)될 수 없는 근본적인 복잡성 (irreducible complexity)을 갖는다고 주장했다.
이를 엔트로피 (Entropy)라고 이름을 붙였다.
또한, 최종 데이터 압축 (Data compression)은 entropy H 를 의미하고,
통신에서의 최종 전송률 (Data rate)는 capacity C 를 의미한다.
Source의 엔트로피가 channel capacity보다 작은 경우,
점진적으로 (asymptotically) 오류가 없는 통신이 가능하다고 주장했다.
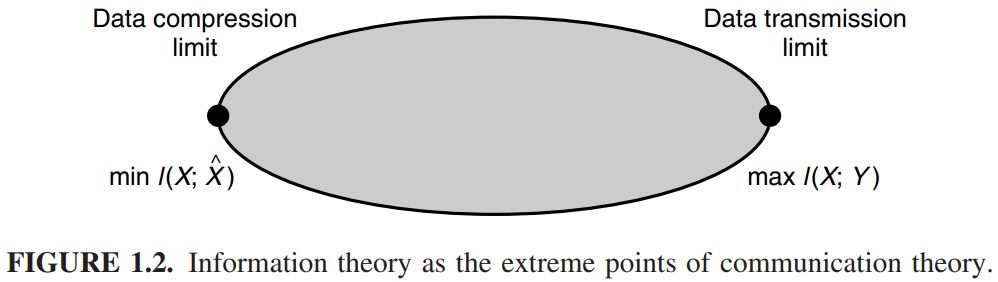
좌측의 맨 끝점은 데이터 압축 (compression)의 minimum을 의미하고,
우측 끝점은 데이터 전송 (transmission)의 maximum을 의미한다.
다시 말해서, 우측 끝점은 channel capacity를 의미한다.
따라서, 통신에서의 모든 변조 (modulation) 방식과 데이터 compression 방식은 이러한 제한 안에 위치한다.
1.3 엔트로피
확률 질량 함수 (probability mass function) p(x) 를 갖는 확률변수 (random variable) X 의 엔트로피는 다음과 같다.
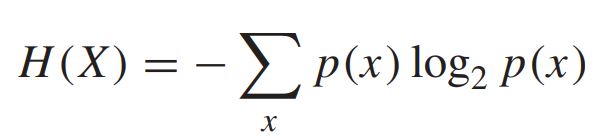
엔트로피를 bit로 측정하기 위해, log의 밑을 2로 한다. 또한 엔트로피는 확률변수의 "평균 불확실성 (average uncertainty)"의 측도이다. 이는 확률변수를 설명하는데 필요한 평군 비트 수를 의미한다.
- Example 1: 32가지 결과에 대해 균일 분포 (uniform distribution)을 갖는 확률변수 X 를 고려하자. 32가지 결과를 나타내기 위해서, 32가지의 다른 값으로 구성된 레이블 (label)이 필요하다. 즉, 5bits의 문자열로도 충분하다.
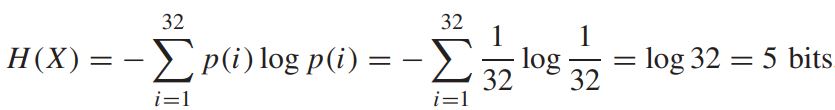
확률변수 X 가 균일 분포를 갖기 때문에, 모든 i 에 대한 확률은 1/32로 동일하다. 즉, 엔트로피는 다음과 같이 구할 수 있다.
- Example 2: 8마리의 말이 참가하는 경마 경기를 생각해보자. 각각의 말이 이길 확률을 다음과 같이 (1/2, 1/4, 1/8, 1/16, 1/64, 1/64, 1/64, 1/64)라 하자. 이때, 경마에서 어떤 말이 이겼는지를 나타내는 메시지를 전송하고자 한다.
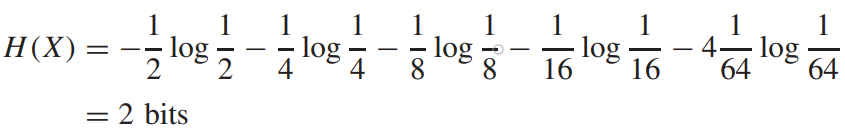
이때의 확률변수 X 는 다음과 같이 말에 따라 확률이 다르기 때문에, 엔트로피를 계산하면 다음과 같이 구할 수 있다. 즉, 이길 가능성이 높은 말에 대해서는 더 짧은 bit를 사용하여 정보를 전달하고, 가능성이 낮은 말에 대해서는 긴 bit를 사용하여 "전체적인 평균 설명 길이"를 줄일 수 있다. 예를 들어, 다음과 같은 비트 문자열 세트로 8마리의 말을 표현할 수 있다.
[0, 10, 110, 1110, 111100, 111101, 111110, 111111]
정보이론에서의 엔트로피 개념은 통계역학 (statistical machanics)에서의 엔트로피 개념과 관련이 있다.
n개의 독립 및 동일 분포 (independent and identically distributed (i.i.d.)) 확률변수 X 의 시퀀스 (sequence)를 구할 때, "typical" sequence의 확률은 다음과 같다.
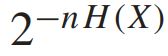
이때, 다음과 같은 수의 typical sequence가 있다.
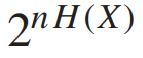
1.4 상호정보 및 채널용량
우리는 엔트로피를 이용하여 다음과 같은 조건부 엔트로피 (conditional entropy) H(X|Y) 를 정의할 수 있다.
여기서 X 와 Y 는 확률변수이다. 이는 다른 확률변수 Y 의 정보를 알고 있는 상황에서, 확률변수 X 의 엔트로피를 말한다.
이렇게, "다른 확률변수로 인한 불확실성의 감소"를 상호정보 (mutual information)이라 정의한다.
mutual information의 정의는 다음과 같다.
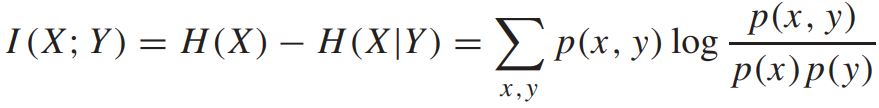
mutual information I(X;Y) 는 두 개의 random variable간의 의존성 (dependence)를 측정하는 지표이다.
I(X;Y) 는 항상 음이 아닌 값을 가지며, X 와 Y 가 독립 (independent)인 경우에만 0의 값을 갖는다.
이제, channel capacity에 대해 정의해보자.
통신채널은 출력 (output)이 입력 (input)에 확률적으로 의존하는 시스템이다. 즉, 입력에 대한 조건부 분포를 결정하는 확률 전이 행렬 (probability of transition matrix) p(y|x) 에 의해 특성화 (characterized)된다.
따라서, channel capacity C 는 input X 와 output Y 에 대한 함수로 다음과 같이 정의할 수 있다.
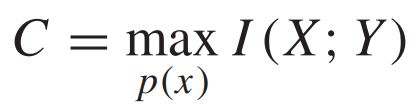
즉, channel capacity란 오류가 발생하지 않으면서 (혹은 오류가 거의 발생하지 않으면서) 정보를 최대한으로 전송할 수 있는 용량을 의미한다.
예제와 함께 capacity의 개념에 대해 살펴보자.
- Example 1: 잡음이 없는 (Noiseless) 이진 (Binary) 채널을 예로 들어보자. 이 채널에서는 binary input이 정확하게 output으로 출력된다. 해당 채널은 다음과 같다. 이와 같은 채널에서는 어떠한 비트라도 에러 없이 수신된다. 따라서, 각 전송마다 1bit를 안정적으로 수신자에게 전송할 수 있으며, capacity는 1bit이다. 즉, C = max I(X;Y) = 1 bit 이다.

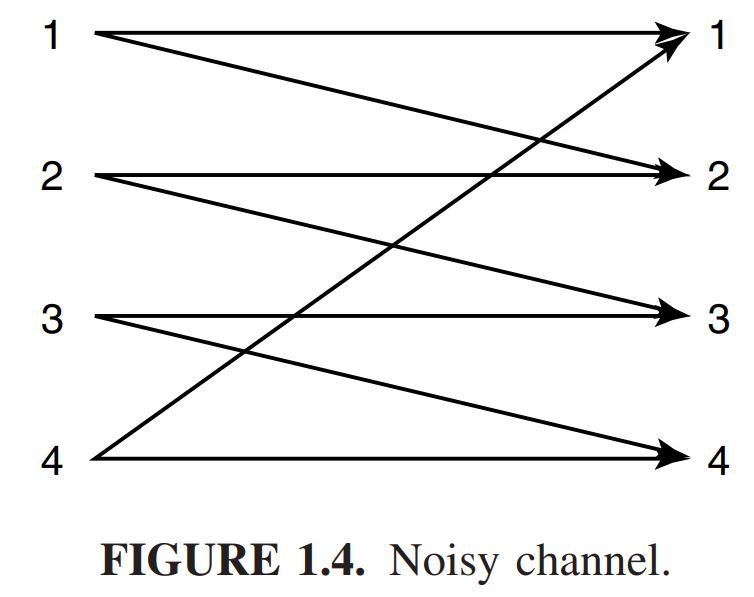
- Example 2: 잡음이 있는 네 가지 symbol 채널을 예로 들어보자. 이 채널에서 각 input symbol은 1/2 확률로 동일한 input을 output으로 출력되거나, error가 발생한다. 해당 채널은 다음 아래와 같다. 이와 같은 경우, output을 분석한다 하더라도, 어떤 input symbol이 전송되었는지 확실하게 알 수 없다. 예를 들어, 내가 수신받은 symbol이 2라고 했을 때, input symbol이 1 혹은 2가 될 수 있기 때문이다.
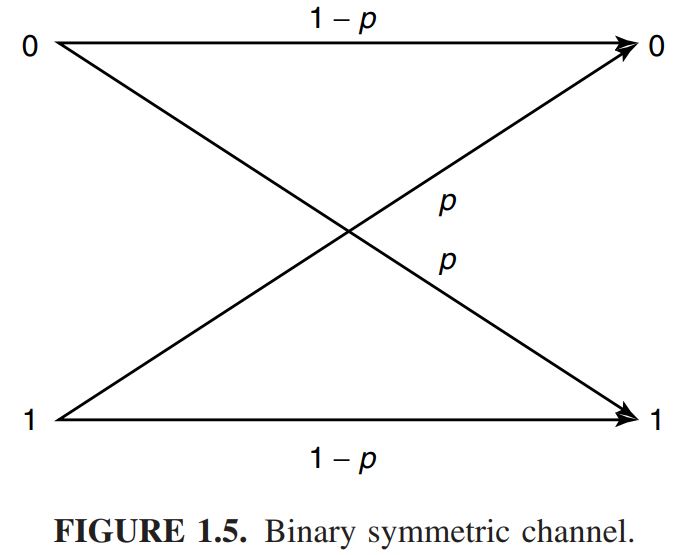
- Example 3: 이진 대칭 채널 (Binary symmetric channel (BSC))을 살펴보자. 이는 noise가 있는 통신 시스템의 기본적인 예이다. 해당 채널은 아래와 같다. 이 채널은 binary input을 가지며, output은 1-p 의 확률로 올바르게 수신되고, p 의 확률로 error가 발생한다. 이러한 경우에서, channel capacity C는 다음과 같다.
C = 1 + p log p + (1 − p)log(1 − p) [bits/transmission]
즉, 통신 속도에 대한 궁극적인 limit는 channel capacity에 의해 결정된다. 특히, 채널 부호화 이론(channel coding theorem)은 이러한 limit를 긴 블록 길이 (long block length)를 가진 부호 (code)를 사용하여 달성할 수 있다는 것을 보여준다.
1.5 상대 엔트로피
Mutual information는 상대 엔트로피 (relative entropy) D(p||q) 라고 불리는 일반적인 양의 특수한 경우라 할 수 있다.
여기서 상대 엔트로피는 확률질량함수 p 와 q 사이의 "거리 (distance)"를 측정하는 지표이다. 이는 다음과 같다.
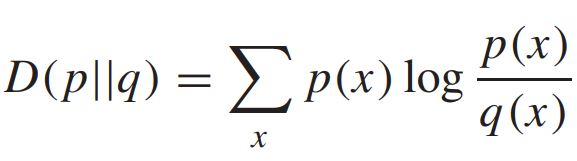
이는 앞에서 mutual information을 설명했던 것과 같이, 항상 음이 아닌 값을 가지며, p = q 인 경우에만 0의 값을 갖는다.
1.6 마무리
지금까지 정보이론의 기초 개념으로 "엔트로피 (entropy)"와 "상호정보 (mutual information)" 및 "채널용량 (channel capacity)"에 관하여 다루었다. 앞으로 다루는 내용에서는 여러 예제를 다루어 개념을 좀 더 자세히 다루고 추가적으로 중요한 이론 및 개념을 소개할 예정이다. 또한, 블로그를 작성하면서 "용어"를 한국어와 영어표현으로 번갈아가며 사용하고 있으므로 주의가 필요하다.
'Information Theory' 카테고리의 다른 글
| 2-2. Jensen's 와 Fano's inequality 및 충분 통계량 (0) | 2023.07.18 |
|---|---|
| 2-1. 엔트로피, 상관 엔트로피 및 상호 정보 (0) | 2023.07.12 |

