출처: https://www.youtube.com/watch?v=_PDyi5BVY-E
Power method란?
Power method의 목적은 어떤 임의의 행렬(matrix)의 가장 큰 고유값(largest eigenvalue)과 이에 해당하는 고유 벡터(eigenvector)를 찾는 것을 말한다. 이에 대한 내용을 담은 강의 주소를 위에 올려두었다.
이제 power method에 대해 설명할 것이다.
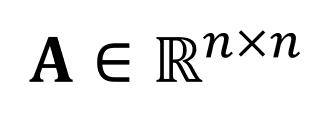
예를 들어, 다음과 같이 $n \times n$ 실수행렬 (real matrix)인 $\boldsymbol{\mathrm{A}}$ 가 있다고 하자.
이때, matrix $\boldsymbol{\mathrm{A}}$ 는 실수 고유값 (real eigenvalues)과 이에 해당하는 eigenvector를 갖고 있으며, eigenvalue의 경우 $n$개의 분명하게(distinct) 구분되는 실수 값(real value)이다.
이제 이러한 eigenvalues가 다음과 같이 나열(ordering) 된다고 가정하자. 즉, 다음과 같이 "크기가 큰 순서대로 정의되어 있다"고 하자. 여기서 람다(lambda) 값은 eigenvalue에 해당하며, 이를 "양수" 혹은 "음수"라고 정의하는 것은 중요하지 않다. 그 이유는 lambda 값이 갖는 의미는 단순히 vector에 대한 "크기"를 의미하기 때문이다.
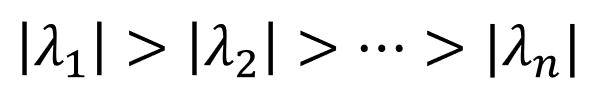
이러한 eigenvalues는 다음과 같은 eigenvectors에 대한 값이다. 여기서 eigenvectors는 서로 선형적으로 독립 (linearly independent) 이다. 즉, $n$개의 linearly independent한 eigenvectors가 있다.

따라서, 어떠한 (any) $n \times 1$만큼의 차원 (dimension)을 갖는 열 벡터 (column vector)로 표현할 때,
위와 같은 $n$개의 eigenvectors의 선형 결합 (linear combination)으로 표현할 수 있다.
1.2 Power method의 예
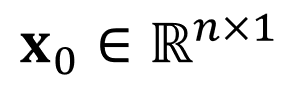
예를 들어보자.
다음과 같이 $n \times 1$의 dimension을 갖는 vector ${\bf{x}}_{0}$가 있다고 하자. 우리는 이러한 vector를 아래와 같이 $e_1$ 에서부터 $e_n$ 까지의 eigenvectors의 linear combination으로 표현할 수 있다.
여기서 $c$ 는 각 eigenvectors의 크기를 나타내는 "real constant" 값이다.
이를 일반 (generation)식으로 표현하기 위해, 합 기호 (summation notation)를 사용하면 아래와 같다.
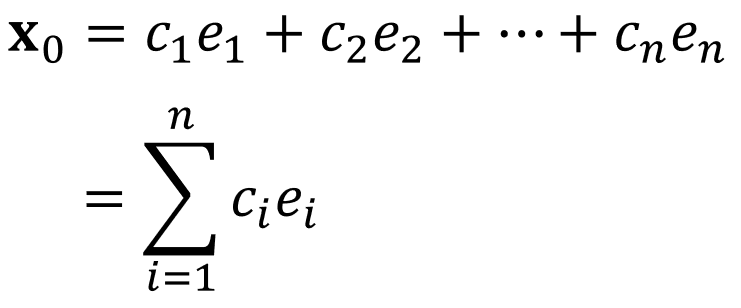
그럼 이제, 이러한 vector에 matrix $\bf{A}$를 곱하면 어떤 일이 일어날까?
Vector ${\bf{x}}_0$에 matrix $\bf{A}$를 곱한 것을 ${\bf{x}}_1$이라 하자. 그럼, ${\bf{x}}_1$ vector는 다음과 같다.
아래 식에서 빨간색으로 표시한 부분을 자세히 보자.
빨간색 박스안의 $e_i$는 "$\lambda_{i}$ 라는 eigenvalue를 갖는 $\bf{A}$의 eigenvector"를 의미한다.
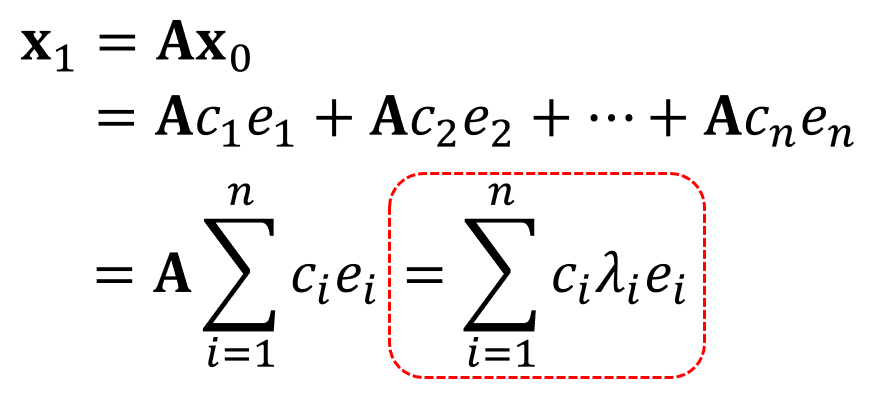
우리는 이와같은 사실을 이용하여 ${\bf{x}}_1$ vector를 다음과 같다고 표현할 수 있다.

즉, matrix $\bf{A}$ 를 곱한다는 것의 의미는 합 기호 안에 있는 각 수식 (term)들과 "eigenvalue"를 곱하는 것과 같다.
이제 다음과 같은 물음을 할 수 있다.
그럼, matrix $\bf{A}$ 를 $p$ 만큼 제곱하여 곱하면 어떻게 될까?
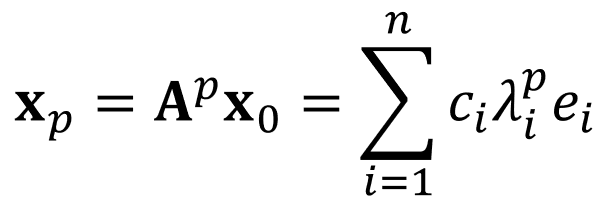
결론적으로, eigenvalue에 $p$만큼 제곱한 형태가 된다.
마지막으로, ${\bf{x}}_p$에 대해서 우리는 어떤 결론을 지을 수 있을까?
맨 처음으로 돌아가서, 우리는 $\lambda_1$이 가장 큰 값을 갖는 고유값(dominant eigenvalue)이라 정의했었다.
따라서, $\lambda_1$에 $p$ 만큼 제곱한 값은 다른 eigenvalue에 $p$를 제곱한 값에 비해 "매우 큰 수"가 된다.
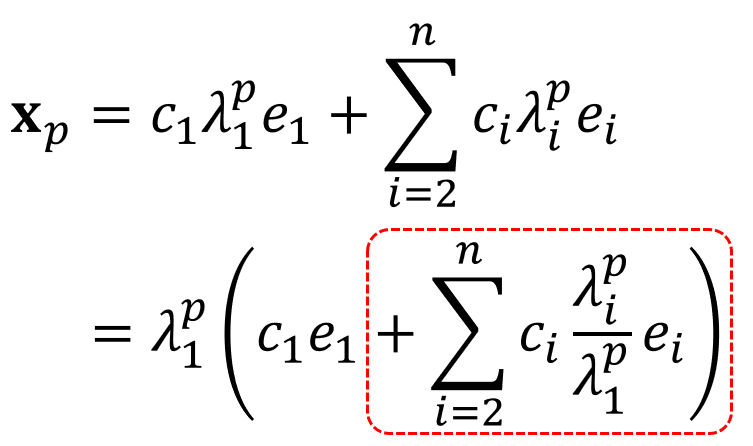
따라서, vector ${\bf{x}}_p$는 다음과 같이 정리할 수 있으며, 첫번째 eigenvalue $\lambda_1$의 값이 다른 eigenvalue에 비해 매우 크기 때문에, 빨간색으로 표현한 부분은 0으로 수렴한다.
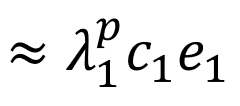
결과적으로, 다음과 같이 근사화 (approximation)되어, dominant eigenvalue와 이에 해당하는 eigenvector를 얻을 수 있다.
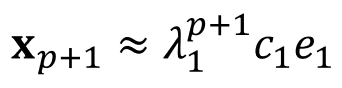
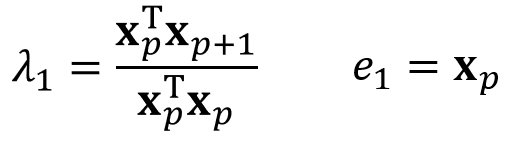
그럼, 우리가 이제 dominant한 eigenvalue $\lambda_1$에 대해서 문제를 풀려고 한다. 이때, 어떻게 문제에 해당하는 $\lambda_1$을 구할 수 있을까? 다음과 같이 $p+1$ 만큼 제곱하여 ${\bf{x}}_{p+1}$을 구하고, 바로 위에서 구했던 ${\bf{x}}_{p}$를 이용하여 $\lambda_1$을 구할 수 있다. 이에 해당하는 eigenvector $e_1$또한 구할 수 있다.
1.3 마무리
$\lambda_1$가 가장 dominant한 eigenvalue이므로, 이를 $p$만큼 제곱하면 다른 eigenvalue $\lambda$에 비해 매우 큰 수로 정의된다.
즉, 행렬 $\bf{A}$와 벡터 $\bf{x}$의 곱으로 이루어진 식이 가장 dominant한 하나의 값 $\lambda_1$과 이에 해당하는 하나의 벡터 $e_1$의 곱으로 표현되며, 이에 해당하는 벡터 $e_1$은 eigenvector이다.